The Catch 2019 writeup

The Catch is an online CTF competition organized by the local internet infrastructure non-profit CESNET.

Last year we placed first as a team and got to attend the Trend Micro CTF finals in Japan. This year the CTF was an individual competition and I managed to get the second place.

The Infiltration
Payment Terminal
Vacuum Cleaner
Colonel Roche

The Infiltration

Here we are provided with a remote HTTP server which returns Python code generating a password and expects the password back in 5 seconds (this is handled by using a session cookie we have to keep around).

Unfortunately the Python code is malformed and changes per each request.

# ... 
ipmort sys  # <- 'import' gets mangled
import argparse
# ...
dfe finalize(code):  # <- 'def' gets mangled
# ...
    if i % 2 == 0  # <- ':' is sometimes missing
        res += v
# ...
    if int(str(init)[0]) % 2 == 0:
    value += "ng"  # <- Indentation is sometimes broken
# ...
        value + = "D5"  # <- '+=' gets mangled

In the end, this was mostly drudge work, figuring out what heuristics are “good enough” to fix the code without breaking it is some other way. I suspect one could harness something like pylama to do a bit more precise fixups, but that was not necessary here.

# ...

def fix_fn(i, fnsig):
    # Fix declaration
    lines[i] = "def " + fnsig
    for i in range(i+1, i+4):
        lines[i] = "\t#"  # Removes docstrings
    # The convert function has an extra newline after its docstring,
    # we change it to a nonempty line to properly detect end of function later. 
    if fnsig == "convert(init):":
        i += 1
        lines[i] = "\t#"

    # Here we iterate until we arrive at the end of a function
    k = i + 1
    while lines[k] != "":
        strip = lines[k].strip()
        # Add missing ":"
        if strip[-1] != ":" and any(strip.startswith(t)
                                    for t in ["for", "else", "if"]):
            lines[k] = lines[k] + ":"

        # Indent can be broken only right at the start of a block
        if lines[k][-1] == ":":
            # Force next line indent
            level = lines[k].count("\t")
            lines[k+1] = "\t"*(level+1) + lines[k+1].strip()
        k += 1
        continue
    # Patch return
    lines[k-1] = "\treturn" + lines[k-1][7:]

# Walk over all lines in the file
for i, line in enumerate(lines):
    lines[i] = line.replace(" + = ", " += ")
    for fnsig in fnsigs:
        if not line.endswith(fnsig):
            continue
        fix_fn(i, fnsig)

# ...

This does not work in all cases, but running the script several times will eventually get a fixable input code that produces the correct result.

Payment Terminal

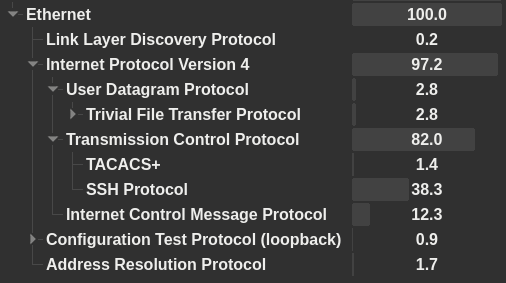
We get a PCAP containing an exchange that captures configuration upload to a Cisco router.

First we look at the TFTP exchange. Following the appropriate UDP stream in Wireshark yields this file:

........
!
! Last configuration change at 14:06:27 UTC Mon Jun 10 2019
!
version 15.5
service timestamps debug datetime msec
service timestamps log datetime msec
service password-encryption
!
hostname Router-R12
!
boot-start-marker
boot-end-marker
!
# ...
# Interesting lines follow (comments added by me)
tacacs-server host 172.16.66.14
tacacs-server key 7 0804545A1B18360300040203641B256C770272010355
# ...

TACACS is some ancient protocol for configuring network devices. Our dump contains it, so we should look at that next.

Fortunately Wireshark supports decrypting TACACS exchanges. Unfortunately the preshared key is in some “encrypted” Cisco format. This can however be easily reversed using this online tool.

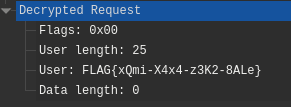
Looking through the decrypted TACACS requests yields the flag as a request parameter.

Vacuum Cleaner

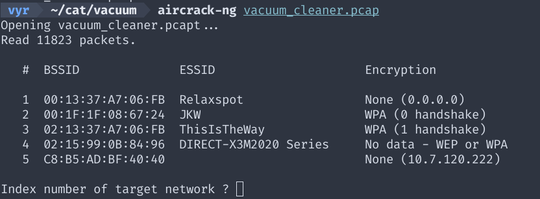
Here we have a PCAP containing a large amount of encrypted 802.11 traffic. Running aircrack-ng shows that it contains an authentication handshake for the suggestively named “ThisIsTheWay” network.

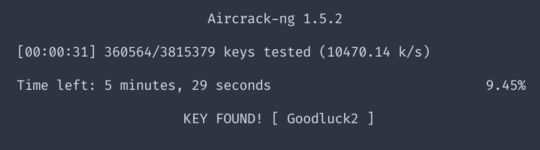
After some messing with wordlists, I got lucky with the one from OpenWall, cracking the password in under a minute.

After configuring Wireshark to use the password to decrypt the Wi-Fi traffic, the flag can be found inside a TXT DNS exchange. For whatever reason, I needed to generate a PSK first instead of entering the password directly.

Colonel Roche

This one definitely took me the longest.

We get the following ciphertext:

463216327617246f67406f1266075ec622606c6671765537066636596
e621e64e622c2b006066961c66e621f067676e77c6e665167a462c4b5
0477433617754222d7043542885747df6dd575970417d435223000

(linewrapping added by me)

We also get reference to someone called “Colonel Roche”. This guy was a French aeronautical engineer who also dabbled in cryptography. Finding any references to his cryptographical work is extremely hard though. An 19th century textbook can be found that references a cipher named after him but as I do not know any French, it was of very little help. The fact that a street named after him exists housing multiple academic institutions does not help the situation at all.

Out of desperation, I attempted to google a result in Czech and bingo, I got a decade old popsci article about “Colonel Roche’s Transposition Cipher”.

As finding anything about this in English is next to impossible, let me reproduce the method here. The cipher is basically a column transposition cipher except that the columns can have variable lenghts.

First we pick a key, such as robot and number each of the characters depending on its alphabetical order. Note that if we have repeating letter, it does not get assigned the same number twice.

|r|o|b|o|t|
|4|2|1|3|5|

Now we construct variable columns with length limited by their appropriate numerical value. Then we start writing the plaintext in the rows. If a row is already at its maximum character count, we skip it.

Here we take colonelroche as our ciphertext.

|4|2|1|3|5|
|c|o|l|o|n|
|e|l| |r|o|
|c|   |h|e|
|-|     |-|
        |-|

Notice that I padded the message with - to fill all columns. This will be important later.

Reading the columns in the top-down order results in the ciphertext cec-ollorhnoe--.

Decryption is just the process in reverse - We fill columns first and then read the rows.

Now we can make an important observation. As the ciphertext is always padded to fill up columns from 1 to the key length $N$ , it’s length $L$ is constrained to be an integer solution of the following:

$L = \frac{N(N+1)}{2}$

Looking at the ciphertext can give us another important clue — the flag has to contain characters like { and if we hex-decoded before applying the decryption, there would be no way of getting those characters. Thus it is clear we have to apply the algorithm to the hexadecimal digits directly.

Now we come to the main issue. We have $L = 168$ digits and as such there is no integer solution for $N$ . The closest we can get is $L(17) = 153$ and $L(18) = 171$ .

At this point I was hopelessly stuck, attempting to rearrange the blocks manually, generating the block sizes using various more or less sane methods. The challenge hints that the key is a day of week, but what if the block sizes are generated from the hexadecimal digits of the key or something.

After a large amount of effort I finally decided to try the obvious — dividing the ciphertext to fixed-size substrings and using the decryption algorithm on them individually, concatenating the result at the end.

For our given $L$ we can divide it with lengths of monday, tuesday, friday and sunday.

Now I just tried all the possible keys and got the result.

for dow in days_of_week:
    key_nums = key_to_num(dow)
    N = sum(key_nums)
    L = len(data)
    if L % N != 0:
        print(dow, "skipped")
        continue

    total = ""
    for i in range(L // N):
        d = data[i*N:(i+1)*N]
        blocks = ciphertext_to_blocks(d, key_nums)
        seri = blocks_to_plaintext(blocks)
        total += seri
    if len(total) % 2 == 0:
        print(dow, binascii.unhexlify(total))
    else:
        print(dow, "Invalid total result length")

monday b'Broadcast on all frequencies and in all known languages:
    FLAG{uB8W-XBtp-OmtE-Q2Ys}\x00\x00'
tuesday b"FvF\xf62\xf0\x13$b'v\x16a\x07Rg0nggl\x01VfS,fYn+\x06
    \x9el\x06fB\x01.l\x16bnfvVrw\xe1\xa1ld\xf7f\x06.\xc4\xb7t\xd0
    EG'05%C$v!\x88_P\xd3WiD$\xd7\x12}s\xd5\x07\x00"
wednesday skipped
thursday skipped
friday b'Broadcast on all frequencies and in all known languages:
    FLAG{uB8W-XBtp-OmtE-Q2Ys}\x00\x00'
saturday skipped
sunday b"Abof\x14c7r$pol a\x06l'&enqseng9e\x06%and in\xc6ab\x0c+
    `n`gn&\xecawoeqg s:\xc4FDqkuuMXW'HB\x02rM?mQE-\x972W\xd3p\x04\x00"

Note that both monday and friday produce the same numerical key.

The Catch 2019 writeup

Contents

The Infiltration

Payment Terminal

Vacuum Cleaner

Colonel Roche